前回紹介したニュートン・
問題 ニュートン・ラフソン法で4x2+12x+9=0 の解を求めましょう。
前回の例題で紹介したソースコードを編集して、
解説
問題 ニュートン・
先ず、
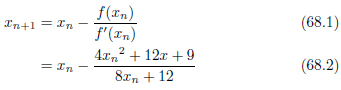
方程式を手で解いた結果は、
漸化式をdouble型の精度いっぱいを目指して計算させるプログラムを次に示します。値が振動する、
//filename : NewtonMethodTest2.java
public class NewtonMethodTest2 {
//---------------------------------
//データ宣言部
static int ShokiTi=1;
static int Kurikaeshi=1000;
/**
* メインメソッド
*/
public static void main (String args []) {
NewtonMethod();
}// end of main()
//---------------------------------
//メイン関数内で利用する関数宣言
//- - - - - - - - - - - - - - - - -
//
static void NewtonMethod(){
double x_p;//漸化式の右側のx 値
double x_s;//漸化式の左側のx値
x_p = ShokiTi;
for(int i=0;i<=Kurikaeshi;i++){
x_s = x_p - (4*x_p*x_p+12*x_p+9) / (8*x_p+12);
System.out.printf
("%4d: %20.18f -> %20.18f\n",i, x_p , x_s );
if (x_s == x_p) {
System.out.println
("精度の限界まで計算しました。e="+ Math.abs(x_s+1.5));
break;
}// of if
x_p = x_s;
}// of for i
}// end of NewtonMethod
}// end of this file...NewtonMethodTest2.java実行結果は次のようになりました。
C:\>java NewtonMethodTest2
0: 1.000000000000000000 -> -0.250000000000000000
1: -0.250000000000000000 -> -0.875000000000000000
2: -0.875000000000000000 -> -1.187500000000000000
3: -1.187500000000000000 -> -1.343750000000000000
4: -1.343750000000000000 -> -1.421875000000000000
5: -1.421875000000000000 -> -1.460937500000000000
6: -1.460937500000000000 -> -1.480468750000000000
7: -1.480468750000000000 -> -1.490234375000000000
8: -1.490234375000000000 -> -1.495117187500000000
9: -1.495117187500000000 -> -1.497558593750000000
10: -1.497558593750000000 -> -1.498779296875000000
11: -1.498779296875000000 -> -1.499389648437500000
12: -1.499389648437500000 -> -1.499694824218750000
13: -1.499694824218750000 -> -1.499847412109375000
14: -1.499847412109375000 -> -1.499923706054687500
15: -1.499923706054687500 -> -1.499961853027343800
16: -1.499961853027343800 -> -1.499980926513671900
17: -1.499980926513671900 -> -1.499990463256836000
18: -1.499990463256836000 -> -1.499995231628418000
19: -1.499995231628418000 -> -1.499997615814209000
20: -1.499997615814209000 -> -1.499998807907104500
21: -1.499998807907104500 -> -1.499999403953552200
22: -1.499999403953552200 -> -1.499999701976776100
23: -1.499999701976776100 -> -1.499999850988388000
24: -1.499999850988388000 -> -1.499999925494194000
25: -1.499999925494194000 -> -1.499999961256981000
26: -1.499999961256981000 -> -1.499999972719412700
27: -1.499999972719412700 -> -1.499999980858702300
28: -1.499999980858702300 -> -1.499999992458992400
29: -1.499999992458992400 -> -1.499999992458992400
精度の限界まで計算しました。e=7.541007596145732E-9解析的に方程式の解を求めると、
考えられる誤差の発生機構は、
試しに、
a = (4*x_p*x_p+12*x_p+9) / (8*x_p+12);
x_s = (x_p*x_p - a*a)/(x_p+a);aはdouble型の一時変数です。このように計算式を変形して実行してみた結果は次の通りでした。
(略)
40: -1.500000008809426000 -> -1.500000008809426000
精度の限界まで計算しました。e=8.809426077505123E-9誤差はわずかに大きくなってしまいました。計算回数が増えたことにより、
では、
x_s = x_p - (0.5*x_p+3.0/4.0);漸化式をこのように式変形することが出来ました。こうしたときの実行結果は次の通りでした。
(略)
54: -1.500000000000000000 -> -1.500000000000000000
精度の限界まで計算しました。e=0.0やりました! double型の精度いっぱいまで追い込むことに成功しました。真の値が分かっている場合には、
結局は、
今回はここまで
ニュートン・



